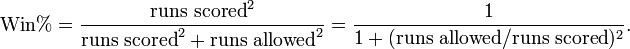Columns

Frozen Assets: A Fresh (Pythagorean) Perspective on Team Rankings

The pythagorean expectation formula is applied to the current NHL standings with some interesting results

by
Ari
December 18, 2009

From Wikipedia:

Pythagorean expectation is a formula invented by Bill James to estimate how many games a baseball team “should” have won based on the number of runs they scored and allowed. Comparing a team’s actual and Pythagorean winning percentage can be used to evaluate how lucky (or alternatively how “clutch”) that team was (by examining the variation between the two winning percentages). The term is derived from the formula’s resemblance to the Pythagorean theorem.
The basic formula is:
$\mathrm{Win\%} = \frac{\text{runs scored}^2}{\text{runs scored}^2 + \text{runs allowed}^2} = \frac{1}{1+(\text{runs allowed}/\text{runs scored})^2}.$
where Win% is the winning percentage generated by the formula. The expected number of wins would be the expected winning percentage multiplied by the number of games played.

Applied to hockey, the formula looks like this:

Win% = (Goals For^2)/((Goals For^2) + (Goals Against^2))

EAST

ATLANTIC	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

New Jersey	32	23	8	1	47	93	69	0.645	111
Pittsburgh	35	24	10	1	49	114	90	0.616	107
Philadelphia	33	15	16	2	32	93	97	0.479	79
NY Rangers	34	15	16	3	33	94	100	0.469	78
NY Islanders	35	13	15	7	33	88	113	0.378	68

NORTHEAST	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

Buffalo	32	20	10	2	42	85	70	0.596	102
Boston	32	16	10	6	38	84	80	0.524	90
Ottawa	33	17	12	4	38	94	96	0.489	86
Montreal	36	15	18	3	33	90	104	0.428	72
Toronto	34	12	15	7	31	100	122	0.402	70

SOUTHEAST	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

Washington	34	21	7	6	48	124	95	0.630	108
Atlanta	33	18	12	3	39	108	99	0.543	92
Florida	35	14	14	7	35	99	115	0.426	75
Tampa Bay	34	11	14	9	31	81	104	0.378	67
Carolina	33	8	19	6	22	82	120	0.318	53

WEST

CENTRAL	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

Chicago	32	21	8	3	45	95	67	0.668	112
Nashville	35	21	11	3	45	101	98	0.515	93
Detroit	34	18	11	5	41	95	89	0.533	92
St. Louis	32	14	13	5	33	78	88	0.440	77
Columbus	35	14	14	7	35	101	121	0.411	74

NORTHWEST	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

Calgary	34	20	10	4	44	98	82	0.588	100
Vancouver	34	19	15	0	38	106	88	0.592	95
Colorado	36	19	11	6	44	104	105	0.495	90
Minnesota	34	17	14	3	37	89	95	0.467	82
Edmonton	34	15	15	4	34	103	109	0.472	79

PACIFIC	GP	W	L	OTL	PTS	GF	GA	EXP WIN %	PROJ PTS

San Jose	35	20	8	7	47	115	93	0.605	104
Phoenix	35	21	12	2	44	89	79	0.559	97
Los Angeles	37	22	12	3	47	111	108	0.514	93
Dallas	34	14	9	11	39	101	105	0.481	85
Anaheim	34	13	14	7	33	95	109	0.432	74

*Note actual points should be higher because the formula does not factor in overtime losses.

Any surprises? Comments? There are certainly flaws with a) the theorem itself (that has been refined numerous times), and b) its application to hockey (doesn’t factor in the overtime loss). But I am not a statistician and this was done for fun not to make any worthwhile predictions. Please feel free to criticize/correct my work. Also, the formula only applies to a team’s remaining games.

Dedicated to Michael Remis

Illegal Curve Hockey

Columns

Frozen Assets: A Fresh (Pythagorean) Perspective on Team Rankings

Subscribe to Podcast